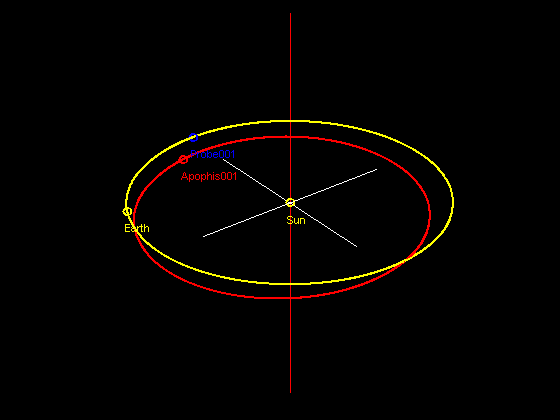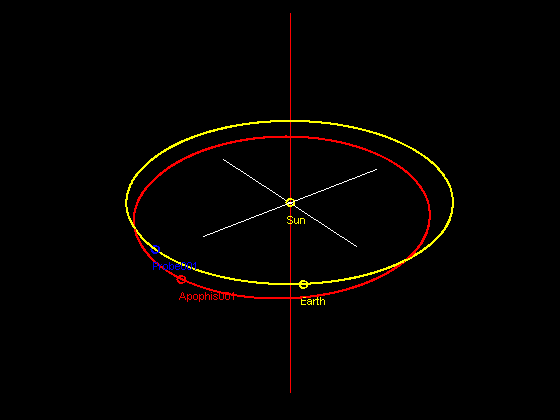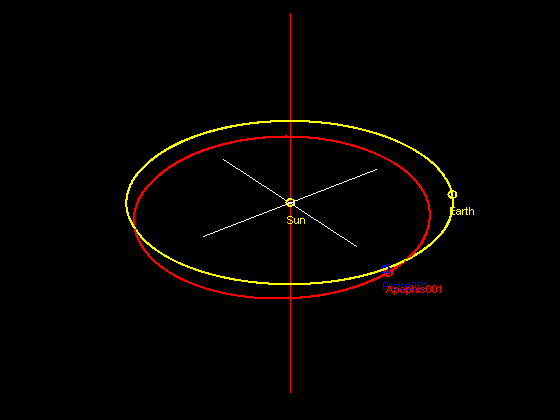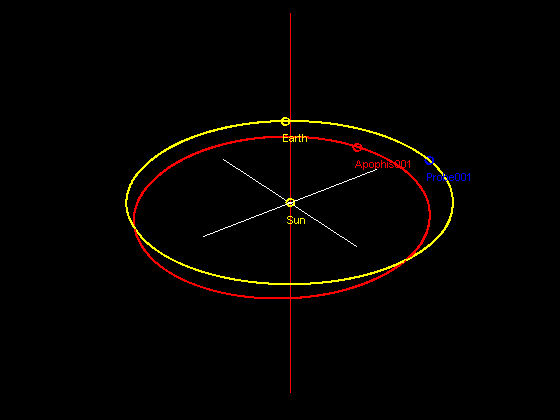
Apophis is one asteroid which crosses Earth's orbit. At one time it held the highest record on the Torino Scale because of a potential collision with Earth in 2029. Since then, the 2029 encounter has been determined to be a near miss. However, there remains a small probability that if the asteroid passes through a "keyhole" in 2029, it can potentially collide with Earth in 2036.
Scientists need more accurate data on the position of the asteroid to determine if the 2029 encounter will indeed pass through the "keyhole". It has been suggested that a probe bearing a beacon can land on the asteroid, much the same way Hayabusa did on asteroid Itokawa. Such a mission is difficult and technologically challenging.
So, instead of measuring the position of Apophis directly using a beacon, can we measure it indirectly? We set up a hypothetical situation, where a probe bearing a beacon is put at the L5 Lagrangian point of Earth's orbit.
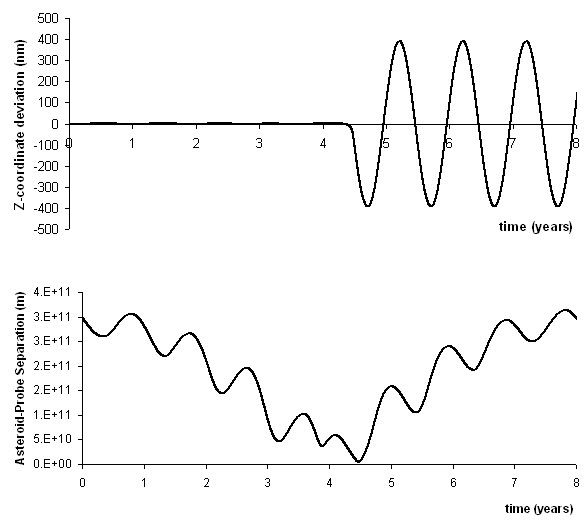
It turns out from the initial conditions stated above, we may hit paydirt in just 4+ years. In 4.5 years, there will be a very close encounter between the probe and Apophis, enough to displace the probe just slightly. This close encounter is shown in the animated gif.
If we plot the displacement of the probe against time, we see that the probe's plane of orbit gets a slight inclination to the ecliptic plane, with the maximim distance above the ecliptic plane at about 300~400+nm.
400nm may not seem like much, but this is on the order of wavelength of light, and possibly this change in distance can be observed with inferometry. It is possible for inferometers to be accurate up to 1/4 wavelength of the light it is using.
The mass of Apophis used is 2.0e10kg, but it can be as much as 4+e10kg, so a first order estimate simply says the distance of 300~400nm can possibly be doubled. This helps in the choice of laser wavelength for the inferometer.